TOF-SANS Working Group

Members

• Andrew Jackson (ESS)
• Anna Sokolova (ANSTO)
• Sebastian Jaksch (ESS)
• Judith Houston (ESS)
• Adrian Rennie (Uppsala)
• Wojciech Potrzebowski (ESS)

News/Status

• Working group formed at canSAS-XI in Freising
• The workshop about TOF resolution was held in March 2021 (online): https://indico.esss.lu.se/event/2506/

Generic resolution function

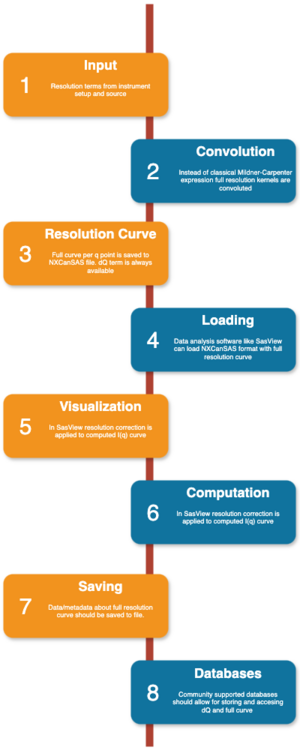
A workflow for utilizing the full resolution curve is shown in figure 1.

Fig. 1. Generic resolution workflow

In order to avoid repetitions and keep the message coherent, bellow I provided mostly the collection of relevant links and current status (March 2024).

• Input data consists of instrumental parameters and shapes of corresponding terms contributing to the resolution function. Please check https://github.com/scipp/esssans/issues/111 for more details
• Convolution. Following developments in GRASP individual resolution kernels are convoluted rather than collapsed to a single number (as classically has been done with Milldner-Carpenter equation). Please review Jupyter notebook on how this can be potentially done https://github.com/scipp/esssans/files/14509637/checkbox-convolution.ipynb.zip
• Resolution curve. The full-resolution curves (defined per q points) are saved to NXCanSAS file. Anticipates entries are /entry/data/q/resolutions and /entry/data/q/resolutions_descriptions. dQ as a single number should always be provided.
• Loading. NXCanSAS files with resolution functions need to be loaded by the analysis software. It will require development in SasView.
• Visualization. Majority of users will probably apply resolution as it is. It may however be useful to be able to plot individual resolution curves and for example, compare it with Gaussian estimates. There may also be some option for changing sampling. This part needs to be defined and developed.
• Computation. Proof-of-concept of applying full resolution curve has been demonstrated using SasView: https://github.com/SasView/sasview/blob/generic_resolution/notebooks/GenericResolutionPOC.ipynb. (Also https://github.com/SasView/sasview/issues/1497)
• Saving. The information about the full resolution curve should be carried on as metadata or the report. It needs to be established
• Databases. It would also be useful if community supported databases can consume this information (both dQ and full description).

Few other open issues not covered with the information above:

In an ideal world the spacings of resolution curve could match the Q spacings of the I(Q) data to save an interpolation step by directly giving the coefficients of the other calculated I(Q) points. But again this should be avoided due to messy issues close to the beam stop, and problems if users crop or rebin data.

The potential solution would be to perform resolution convolution so the model fit Icalc(Q) is interpolated to match the Q values. Ideally, the fitting code would recalculate I(Q) at precise points, or at least on a finer grid, if sharp features are either found or expected.

CHECK: This is the opposite of what Sasview does at present, which is to calculate the value of the Gaussian resolution for a given Q at the adjacent Q values already available for I(Q).

Also need to think about whether to use anything more advanced that Trapezium Rule for the integrations.

TODO: think about Q resolution for 2d data!